James Cook's Homepage


Note there is a complete schedule posted further down this page which shows both office hours and my teaching schedule.

  • Hyperbolic map visualizing tool Hyperbolic Mapper Beta Version (11-17-23, Philip Perry)


    • Spring 2024:

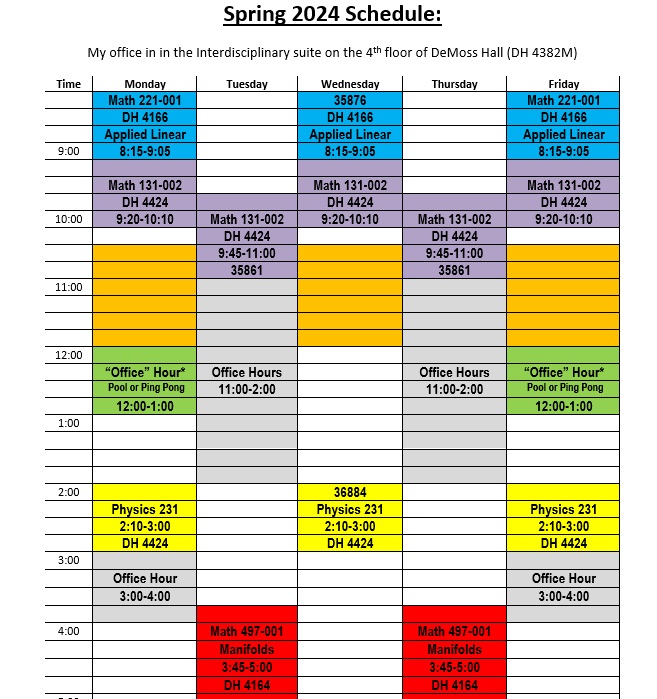
    My Schedule.



    Fall 2023:

    Spring 2023: (note to self: add files here)
    Here are links to the course webpages and You Tube playlists for the courses I intend to teach in the Spring 2023 term:

  • Calculus II (Math 132-002 of Spring 2023) Playlist on You Tube: and Course Website

  • University Physics I (Physics 231-001 of Spring 2023) Playlist on You Tube: and Course Website

  • College Algebra (Math 121-004 of Spring 2023) Playlist on You Tube: and Course Website

  • Introduction to Hilbert Spaces (Math 495-060 of Spring 2023)

  • Lie Algebras

    • Fall 2022: (note to self: add files here)
    Beware the rickroll.
    Spring 2022:

    Fall 2021:

    Spring 2021:
    Fall 2020:

    Recent Research:
    These papers result from work done in conjunction with undergraduates in recent years. I should mention, Nathan BeDell has several papers which support our A-ODE paper. Nathan's papers also give some excellent ideas about future projects in what we might call the precalculus of A-calculus.
    Past Playlists from Courses Taught at Liberty University:

    Links I Recommend:
    1. The ArXiV.
    2. mathstackexchange: a place to learn math and earn reputation.
    3. mathoverflow: research math questions.
    4. My You Tube Channel (has playlists for most recent courses I've taught).
    5. Whistlin Diesel You Tube Channel: the man, the legend, the American.
    6. An intelligent look at the efficacy of masks: Concerning the "science" of masking.
    7. The DATA says no: mask mandates don't make a difference with COVID infection rates.
    8. Great graphs to illustrate the irrelevance of masks to the evolution of COVID infection in diverse populations: I know, I know BUT THE CDC... yes, why believe science when you can believe the totally political CDC ?
    9. On vaccines and abortion: do you think it is ethical to take medicine created by murdering humans? This website gives us some facts we ought not ignore.
    10. Blog & Mablog: sage advice from a post millenial optimist.
    11. Evidence of Election Fraud in 2020.
    12. easy way to save You Tube videos. feel free to save mine, I care not.
    13. Safe and Effective Vaccinations and Mask Measures a short compendium of sources which call into question the wisdom of the current medical establishment.
    Lecture Notes:
    The files posted below are lecture notes from some previous courses that I've taught. I usually update the course notes each time I teach. I post these here for reference sake. My apologies for the errors. If you would like the source LaTeX for these notes feel free to ask, I'm happy to share, my email is jcook at uwa.edu.
    1. Elementary Differential Geometry:[summer 2015, 1/3 done]
    2. Linear Algebra [notes for Spring 2015]
    3. Guide to Gamelin [notes on Complex Analysis from Fall 2014]
    4. More than Complex Variables [notes on Complex Analysis from Fall 2018 in which I did some A-Calculus]
    5. Multivariable Calculus [notes from Calculus III (updated Fall 2014)]
    6. Differential Equations [notes updated Spring 2014]
    7. Differential and Integral Calculus of One Variable [notes for Calculus I (updated Fall 2013)]
    8. Advanced Calculus [notes from Fall 2013]
    9. Applied Linear Algebra [notes from Math 221 from Fall 2012]
    10. Oldschool Calculus I and II [notes from Calculus I and just the first part of II (updated Fall 2011)]
    11. Transition to Advanced Mathematics [notes from Spring 2009]
    12. Mathematical Models in Physics [notes from Ma 430 at NCSU]
    Past Teaching:
    1. Math 423 (online) Resource page
    2. (Math 121) College Algebra.
    3. (Math 221) Applied Linear Algebra.
    4. (Math 321) Linear Algebra.
    5. (Math 421) Abstract Algebra
    6. (Math 422)(2017) Abstract Algebra II
    7. (Math 422)(2009) Abstract Algebra II.
    8. (Math 200) Transition to Advanced Mathematics.
    9. (Physics 231) University Physics I
    10. (Physics 232) Physics II: Electricity and Magnetism.
    11. Introduction to Mathematical Physics.
    12. (Math 126) Applied Calculus
    13. (Math 131) Calculus I.
    14. (Math 132) Calculus II.
    15. (Math 231) Calculus III
    16. (Math 334) Differential Equations
    17. (Math 307) Number Theory.
    18. (Math 497) Special Topics in Elementary Differential Geometry.
    19. (Math 331) Complex Analysis
    20. (Math 332) Advanced Calculus
    21. (Math 495) Special Topics in Geometry
    22. (Math 450) Math Capstone Course.


    Independent Study Courses:
    If a student wishes to learn material past the standard core course at my school and it happens that their interest aligns with my own then I try to set up a Math 495 course with an appropriate title. In order to justify such a course the student needs to have a very solid academic history.

  • Fall 2023: Ernesto Ugana Santana took course in Math 332, taught at higher level that usual, included material from Math 334 as well. Also, met in summer on supermath and A-Calculus. Hope to finish paper on fermionic manifolds with nontrivial topology in Spring 2024 semester.
  • Summer 2023: Philip Perry met and we discussed creation of webtool to visualize hyperbolic mappings. Preliminary version can be seen here: Hyperbolic Mapper Beta Version (11-17-23, Philip Perry)
  • Spring 2023: special topics hybridized course in Hilbert spaces with Jacob Gordon and Audrick Pyronneau. Held course at Liberty, Audrick met via Zoom.
  • Fall 2020-Spring 2023: worked with Audrick Pyronneau on a variety of special topics courses including A-Calculus, topology, Lie Algebras and Hilbert Spaces.
  • 2019-2020: work with Nick Bampton on graph theory and Matlab, tinkered some in topological data analysis
  • Fall 2018: Khang Nguyen and I will likely work on an assortment of A-Calculus and supercalculus topics as time allows.
  • Spring 2018: Khang Nguyen,Cooper Ramsey, Jess Gregory and Johnathan Henney met weekly in a Math 495 course to discuss the A-Calculus project.
  • Fall 2017: nothing formal, but, I plan to work with Khang Nguyen and Cooper Ramsey on a couple ongoing projects in A-Calculus, or, maybe I'll relax.
  • [Daniel Freese, Spring 2017] worked out remaining details of our A-Calculus paper including the theory of power series. We also worked out a number of interesting supermanifolds with nontrivial topology in the fermionic part of the space.
  • [A. McDaniels, C. Ramsey, L. Stacey, B. Hoogerwerf, Fall 2016] gave Honors projects which fit into the A-Calculus research program.
  • [Cooper Ramsey and Jess Gregory, Fall 2016] Math 495 course on PDEs with a focus on Green's functions for Cooper Ramsey and Jess Gregory. We used several texts; Logan, Habermann, Nagle Saff and Snider. A currently incomplete record of what we talked about it given by this You Tube playlist
  • [Daniel Freese and Jess Gregory, Spring 2016] studied elementary topology from Manetti's text, contraction mappings and existence theorems from Chapter 13 of Nagel Saff and Snider's DEqns text, and then we spent a few weeks discussing manifolds. At the conclusion we studied a bit about supermanifolds. See this video record of our meetings
  • [Daniel Freese and Bradley Hoogerwerf, Spring 2016] studied matrix Lie groups. We started with Stillwell's Naive Lie Group text, but, after a few weeks we transitioned to working through the first few chapters of Hall's Lie Groups, Lie Algebras and Representations. Playlist of our meetings .
  • [Daniel Freese, Fall 2015] plan to study A-calculus in depth to continue and refine work initiated with Bailu Zhang.
  • [R.M. Shumate, Spring 2015] plan to study topology from Munkres and Elementary Differential Geometry from Oneill.
  • [Bailu Zhang, Fall 2014] we are studying Cartan for Beginners by Thomas and Ivey as we hope to add some depth to our previous work on the calculus of A-algebras.
  • Spring 2014 I taught a special topics course on Elementary Differential Geometry from Barrett Oneiil's text. There were 7 students. Unofficially, Minh Nguyen worked on Lee's text on Smooth Manifolds and he gave an introductory talk on Coarse Geometry.
  • [Jesse Keyton, Fall 2013] Introduction to Topology (mostly Dr. Skoumbourdis' work here)
  • [Jesse Keyton and Michael Shumate] Abstract Linear Algebra.
  • [Spencer Leslie, Spring 2013] Introduction to Classical Field Theory. (actually, we only got to fiber bundles and connections, classical field theory is a bit past where we got). Spencer turned his focus to measure theory with Professor Skoumbourdis and a project in analytic number theory with Professor Ethan Smith.
  • [Spencer Leslie, Fall 2012] Supermath: an introduction. Worked through the basics of supermathematics including superanalysis and supermanifold theory.
  • [Spencer Leslie, Spring 2012] Topology and Geometry with Dr. Honore Mavinga (Spring 2012). (actually, I just listened to the topology in here, Professor Mavinga did the teaching from Willard's Topology text, then we covered several chapters from Conlon and in the start of the summer we worked through some Riemannian geometry from Burns and Gidea's text.)
  • [Scott Taylor, Spring 2010] Advanced Classical Mechanics (we looked at Saletan's Classical Mechanics, but then we diverged into Cantwell's text on Symmetry and Differential Equations).

    • Older Lecture Notes and Special Discusssions:

    The notes below are older versions.
    1. Calculus I and II. Calculus II's chapters 15 , 16 , 17 , 18 , 19 were reformatted from earlier, inferior, word formatted notes.
    2. Calculus III: multivariate calculus.
    3. Lecture Notes for Applied Linear Algebra (2012 version)
    4. linear algebra (2010 version) paired with Lay's text.
    5. linear algebra (2009 version) paired with Insel,Spence, Friedberg's basic text.
    6. advanced calculus (Fall 2011) based on Edwards, Munkrese, Burns and Gidea as well as notes from R.O. Fulp.
    7. advanced calculus (2009-2010) based on Edwards primarily with more focus on applications, included chapter on variational calculus. Missing examples found here. These notes were compiled from one offering of the course as well as several independent studies given in subsequent semesters.
    8. (2013)advanced calculus, DEqns, manifolds a series of discussions with several students over the summer "break" DEqns and limits Multivariate MVT Contraction Mapping, Newton's Method tensors, wedges, multilinear algebra tensors remix, differential forms manifolds and tangent spacesthese conversations partly inspired the 2013 revision of the Advanced Calculus course.
    9. (2010)advanced calculus with some analysis from Rosenlicht's Introduction to Analysis text. From a focused hybrid 332/422 course with a student who went on to graduate school.
    10. Mathematical Models in Physics: Relativistic Electrodynamics and Differential Forms (from NCSU)
    11. complex analysis. Examples are given in the scanned version. The course went much further, these notes are unfinished.
    12. differential equations (first order ODEs, n-th order problem, systems, series) also concerning the connection between Green's functions and the transfer function.
    Links to websites that do the math for you:
    1. Sage: when in Sage mode you can't be stopped. Notice, you can do Sage online without installing anything locally.
    2. Wolfram Alpha: careful, may be addictive.
    3. Calculates the ref, rref, inverse and much more all while showing all the steps. very nice for problems without ugly decimals.
    4. Eigenvector calculator, ugly numbers no problem. Also deals with complex case no problem. However, does not find generalized e-vectors.
    5. Gram-Schmidt orthogonalizer: by Lawrence E. Turner of Southwestern Adventist University.
    6. matrix multiplier: it's ok, but, has annoying adds
    7. complex number polar form finder: it's ok, but, has annoying adds
    8. automatic algebra website by Daniel R. Collins: check your skill under time pressure. Fun!
    9. cycle notation generator by James Hamblin (check notation against your text before getting too carried away)
    10. subgroup lattice and cayley table generator, by John Jones, I have crashed it before, but usually it's a great resource.
    11. euclidean algorithm for integers thanks to W.J. Cook of Appalachian State U. (aka Bill)
    12. euclidean algorithm for polynomials thanks to W.J. Cook of Appalachian State U. (aka Bill)
    13. phase plane plotter for autonomous system of ODES: pplane plotter, nice and simple
    14. slope field plotter, via geogebra, beautiful
    15. Riemann sums illustrated (also visualizes other things if explore)
    16. really nice calculus III graphing applets, includes some vector fields along a surface as well as cross-sections. This is the best I've seen of this type.
    17. parametric plotter needs flash, worked for me 8-8-17.
    18. 3D-plotter pretty, allows number of different plotting methods and can add vector fields etc... lots of options.
    19. GeoGebra demos. another free math program to learn.
    20. This is how to use GeoGeobra. this website is just art, really pretty.

    Liberal Arts:
    1. paper on Killing's work: by J. Coleman
    2. generatingfunctionology: by Herbert S. Wilf
    3. A Russian Teacher in America: Andrei Toom's amazing criticism of modern "education"
    4. Five Stages of Accepting Constructive Mathematics: Andrej Bauer
    5. Lockhart's Lament: on the abuse of math.
    6. some quotes pulled from Edward Frenkel's "Love and Math".
    Mathematical Distractions:
    1. Gudermannian function the "transcendent angle" a less known bridge between complex and hyperbolic functions
    2. Jacobi's Formula: differentiating determinants and such...
    3. Rigged Hibert Space: as in, it's not fair, nature is rigged
    4. phasors: not the dangerous kind
    5. Smith normal form: how to make row reduction harder, add column operations...
    6. finitely presented abelian groups Chapter 10 Christopher Cooper's really clear notes.
    7. homogeneous equation over system of equations on ring: a basic module theory calculation.
    8. when is there just units or zero divisors Question by Bill on Math Overflow
    9. link to online copy of Lam's Lectures on Modules and Rings, a Springer GTM
    10. geometry of differential equations and Pfaff's Theorem.( bigger picture or see a proof of Pfaff's Theorem)
    11. introductory survey of supermanifolds lots of helpful insights.
    12. Question and Answers about multivariable calculus and differential forms
    13. The local functors of points of supermanifolds: L. Balduzzi, ,C. Carmeli, R. Fioresi
    Random Links:
    1. Wu Tang Name Generator this website proves my Wu-Tang equivalence to Batman.
    2. problem lists nice set of problems on wide range of math
    3. AMS page for undergraduates: thinking about math gradschool?
    4. journals for undergraduate research: links from BYU.gradschool?
    5. how to write your first math research paper in under 5 minutes.
    6. Sophisticated notes on your basic courses.
    7. The "Graph" program I am fond of for creating figures in my notes.
    8. Proof that the Pythagorean Theorem is false.
    9. On topology and breakfast.
    10. Some interesting math reading about maps of the globe.
    11. radian measure, philosophy or quantitative question you be the judge.
    12. I will Derive:math lyricism meets classic a pop tune.
    13. list of the best online math videos sphere inside-out etc...
    14. Financial Math Expert David Prager's Hiking Blog:
    15. Singapore Math: a review by Cathy Duffy. This curriculum I recommend if you are serious about teaching your kids math. It is not easy much like most things worth doing.
    LaTeX (for mathematical documents):
    1. overleaf website (formly writelatex.com) this website is amazing. Although a local installation is faster, this allows us to share and jointly edit LaTeX documents.
    2. just draw the symbol and it finds the LaTeX code for you, this is a nice idea!
    3. the polynom-package for slick long-division in LaTeX, not w/o bugs, found error in calculus II notes as consequence.
    4. LaTeX help wiki. Lot's of nice code.
    5. LaTeX, more from a typesetting professional viewpoint.
    6. on matrices in LaTeX.
    7. LaTeX graphics, this looks tenable, start here when I try again.
    8. advanced graphics tinkering in LaTeX, I'm not there yet, I may never get there...
    9. LaTeX Beamer tutorial, slick LaTeX-based slides.
    10. Tikz introduction article: would be nice to learn...
    Departments, Organizations and Contests:
    1. NCSU department of Mathematics.
    2. American Mathematical Soceity.
    Past Meetings with Students:
    If you are interested in attending a local math meeting sometime this semester please let me know. I don't go as often now since the universities travel policy now requires me to rent a car rather than drive my own. Anyway, if you ask early enough we may find the time to make a trip a reality. Usually the department goes to the MAA meeting each Fall or Spring.
    1. (PaNTS XVIII): Palmetto Number Theory Series at Wake Forest University September 15-16, 2012.
    2. (SUMS)Shenandoah Undergraduate Mathematics and Statistics Conference at James Madison University on Saturday, September 29, 2012
    3. (MAA) The Mathematical Association of America Maryland-District of Columbia-Virginia Section, October 26-27, 2012.
    4. The 8th Annual UNCG Regional Mathematics and Statistics Conference, Saturday, November 3, 2012.
    5. (MAA) The Mathematical Association of America Maryland-District of Columbia-Virginia Section, November 1-2, 2013.
    6. (AMS/MAA) Joint Math Meetings, Atlanta Georgia, January 3-7, 2017.


    Links of interest to past and present students:

  • Old NCSU webpage, many solutions posted.
  • Previous LU course webpages


    • Research and Personal Interests:
    My thesis is in the area of supermathematics. However, recently my interests have also turned to hypercomplex analysis which I refer to as A-Calculus. Projects I'm currently working on:
    1. a text on supercalculus in collaboration with R.O. Fulp
    2. a solution to various inverse problems in A-Calculus with Professor Elifalet Lopez Gonzalez
    3. a paper on elementary differential equations with William J. Cook of Appalachian University
    4. Graph Theoretic data analysis project with Marc Salas and Nick Bampton and...
    Let me share a bit of history on how I began working on A-Calculus. In summer 2012 some meetings with Minh Nguyen prompted the intiation of the research project on the calculus over an algebra. After numerous meetings with Minh, Spencer joined us in about July of 2012. Finally, a bit later Bailu joined in an did some explorations with Maple. In total I'm pleased with the result our group found and it is to be published in a Springer conference proceeding which documents some of the reports given at The 8th Annual UNCG Regional Mathematics and Statistics Conference, Saturday, November 3, 2012. In short, we solved the problem to our satisfaction for any associative semi-simple algebra over the real numbers. Much of what we discovered was known to researchers in the 1950's and we were pleased to discover good agreement. We believe the generalization of the Laplace equation due to Spencer is actually a new idea in this study. Bailu and I have developed material beyond the publication however there was a flaw in our major result which Nathan BeDell found in Summer of 2016. I hope to finish the work I started with Bailu in time, but I've grown to believe a much deeper understanding of A-Calculus is needed to properly finish the project.

    For future students I have several questions from our study of calculus on associative algebra which are still open. I am also interested in differential geometry, it just happens my current obligations have pushed my efforts elsewhere. Thus I have no clear questions for diffential geometry at this time, but if you are interested in that direction of study we can probably find something to work on. If you are interested in undergraduate research (with me) then visit me sometime so we can talk about your background and future plans. Thinking beyond work at LU, it's wise to seek an REU (Research Experience for Undergraduates, funded by the NSF) as soon as possible, don't assume you need all the math courses. There are some REU's that seek students who are between Freshman and Sophomore year. In recent years, we've had math students participate in REU-type programs at Penn State and NCSU.

    I should mention, I do have many questions in supermathematics. However, you need to take all the required courses at LU before we can even properly begin to develop background so we can then discuss the questions. So, this means it is a rare student who has the option to attempt this. Ideally, I'll find some free time to distill the questions down to a form which doesn't require all the background. Sadly, at the moment, I am not there. So I recommend the other questions for the time being.

    From previous semesters: My apologies to the undergraduate who reads through the pages linked below. There is a fair amount of jargon mixed into some of them. I would be happy to explain in more detail any item or phrase you find curious. To the expert who is for whatever reason bored and perusing this site I welcome corrections and/or questions via email (testbetter@yahoo.com).
    1. My Thesis
    2. Talk at AMS meeting at NCSU, Raleigh NC, April 5 2009
    3. Talk at Mid-Atlantic Algebra Conference at NCCU, Durham NC, April 21 2007
      4. The links below contain some rough comments about the topics which occupied my attention in graduate school in physics and math.
    4. Some motivations for supermathematics from physics.
    5. How I first learned of supersymmetry
    6. Superfields; some technical motivations for supermathematics from physics.
    7. Noncommuative superspace (digression from other items)
    8. Random physics topics I enjoy.
    9. Supermath, just the math. (good source of open problems for ambitious undergraduates in math)
    10. An invitation.


    Fun Pictures:

    Hannah reads with Ben Isaac reads with Ben Ben 6 months old Matt Mad

    Matthew plays with Ben

    disney world Lego Store in Disney Springs disney world

    disney world disney world disney world 6 weeks of my summer

    disney world disney world disney world disney world

    disney world disney world disney world disney world

    disney world disney world disney world stupid legoland

    Hannah in SHOES! geometric superspace Hannah Driving! Hannah Driving! Hannah Smiles!

    Axx+ayy+zz=1



    Many thanks to the students who found me meme-worthy:
    My Schedule.




    DISCLAIMER:
    The content and opinions expressed on this website are not necessarily those of Liberty University of Lynchburg Virginia, for more information as to the expressed opinions, beliefs and foundational core values of Liberty University one may consult the official website for details. The primary purpose of this site is to provide my students (and myself) with a permanent easy to find archive of coursework done under my supervision. Also, it serves as an advertisement for my math/physics research hence the site name. Any questions, comments or clarifications may be sent to testbetter@yahoo.com, Thanks.

    Last Modified 3-16-2024.